Refraction of Light, Class – 10 Physics

Introduction :

In our dailylife, we may observe that the path of the rays of light have been bent when the these go from one medium to another medium at the separation of the two media. A man sees a fish under water. He tries to catch it but the fish senses the wave produced due to movement of hand in water by its lateral line and it runs away in another direction for safety. Why the man fails to catch the fish? Why the fish does not appear in its original position ? Why the stars appear to be in a position different from its actual position? In this chapter, we will discuss the phenomenon of light related to the answer of the above questions.

When a ray of light travels from one medium to another medium, due to change in density of the medium, the speed and wavelenght of the light wave change. For these reasons, the light bents at the interface of the two media. The bending of the light rays at the interface of the two media is called as the Refraction of light. Let’s discuss about reflection of light in details.

https://youtu.be/d7aTqolqapA

Definition of Refraction of Light :

The phenomenon of light in which the path of the light rays abruptly change at the separation of two media, is called as the Refection of Light.

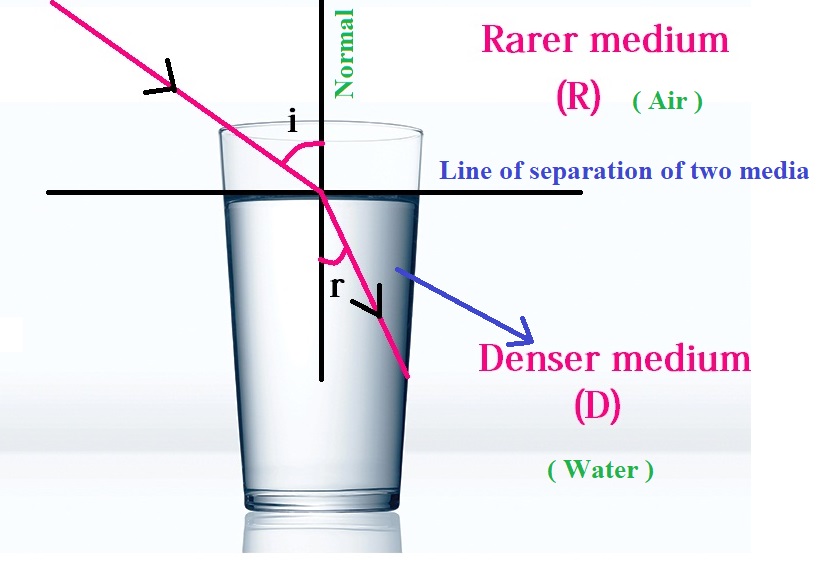
Laws of Refraction of Light :

1 ) The incident ray, point of incidence, normal and refracted ray of light are coplanar.

2 ) The ratio of sine of angle of incidence and angle of refraction is constant. ( This constant term is nothing but the refractive index of the medium )

i.e, sin i / sin r = constant

Where i = angle of incidence

r = angle of refraction

Note : The sencond law of refraction of light is called as the Snell’s Law.

Refractive Index :

According to Snell’s law of refraction of light, the refractive index of a medium is nothing but the ratio of sine of angle of incidence to the angle of refraction. Actually it represents the density of a medium with respect to other medium.

There are two types of refractive index of a medium.

1 ) Absolute Refractive Index

2 ) Relative Refractive Index

Let n₁  = refractive index of rare medium

n₂ = refractive index of denser medium

Refractive index of rare medium with respect to denser medium = ₂n₁ = n₁ / n₂

Refractive index of denser medium with respect to rare medium = ₁n₂ = n₂ / n₁

₁n₂ * ₂n₁ = 1

Example 1 : Calculate the refractive index of galss with respect to water if n_glass = 1.5 and n_water = 1.33

Solution :

Given that, n_glass = 1.5 and n_water = 1.33

Refractive index of glass with respect to water = n_glass / n_water = 1.5 / 1.33 = 1.128

Example 2 : Calculate the refractive index of water with respect to glass if n_glass = 1.5 and n_water = 1.33

Solution :

Given that, n_glass = 1.5 and n_water = 1.33

Refractive index of water with respect to glass = n_water / n_glass = 1.33 / 1.5 = 0.887

Example 3 : Calculate the refractive index of galss with respect to diamond if n_glass = 1.5 and n_diamond = 2.4

Solution :

Given that, n_glass = 1.5 and n_diamond = 2.4

Refractive index of glass with respect to diamond = n_glass / n_diamond = 1.5 / 2.4 = 0.625

Example 4 : Calculate the refractive index of diamond with respect to glass if n_glass = 1.5 and n_diamond = 2.4

Solution :

Given that, n_glass = 1.5 and n_diamond = 2.4

Refractive index of diamond with respect to glass = n_diamond / n_glass = 2.4 / 1.5 = 1.6

Relation between Refractive Index of a Medium and Speed of Light in that Medium :

Let n = refractive index of a medium

v = speed of light in that medium

c = velocity of ligt in space or air or vaccum

n = c / v

n ∝ 1 / v

Hence, the speed of light varies inversely with the refractive index of a medium. That is,

n₁ / n₂ = v₂ / v₁

Example 1 : Find the value of speed of light in glass if the ray of light passes through air into glass. Given that, n = 1.5 and c = 3 * 10⁸  m / s

Solution : Let v = speed of light in glass.

We know that, n = c / v

1.5 = 3 * 10⁸  / v

v = ( 3 / 1.5 ) * 10⁸

v = 2.0 * 10⁸

Hence , required speed of light in glass is 2 * 10⁸ m / s

Example 2 : Find the value of speed of light in water if the ray of light passes through water into glass. Given that, n_glass = 1.5 and n_water = 1.33 and v_glass = 2 * 10⁸  m / s

Solution : Given that,

v_glass = 2 * 10⁸  m / s

v_water = ???

n_glass = 1.5 and n_water = 1.33

We know that,

n_glass / n_water = v_water / v_glass

1.5 / 1.33 = v_water / ( 2 * 10⁸ )

v_water = ( 1.5 / 1.33 ) * ( 2 * 10⁸ ) = 2.25 * 10⁸

Therefore, the speed of light in water is 2.25 * 10⁸ m / s

Example 3 : Calculate the value of refractive index of glass if the light travels from glass to water. Given : n_water = 1.33 and v_glass = 2 * 10⁸  m / s and v_water = 2.25 * 10⁸ m / s

Solution : Given that, n_water = 1.33

v_glass = 2 * 10⁸  m / s

v_water = 2.25 * 10⁸ m / s

We know that,

n_glass / n_water = v_water / v_glass

n_glass / 1.33 = ( 2.25 * 10⁸ ) / ( 2 * 10⁸  )

n_glass= ( 2.25 / 2 ) * 1.33

n_glass= 1.125 * 1.3

n_glass= 1.49625 ≈ 1.5

The required refractive index of glass is 1.5

Relation between Wavelength of Light Rays in two different Media :

Let n₁ = refrative index of incident medium

n₂ = refractive index of refractive medium

λ₁ = wavelength of light in incident medium

λ₂ = wavelength of light in refractive medium

v₁ = speed of light in incident medium

v₂ = speed of light in refractive medium

Since, frequency remains constant during the refraction of light,

v ∝ λ

v₁ / v₂ = λ₁ / λ₂——————————————- ( 1 )

and we know that

v ∝ 1 / n

v₁ / v₂ = n₂ / n₁ ————————————– ( 2 )

By comparing equaitons ( 1 ) and ( 2 ), we get

λ₁ / λ₂ = n₂ / n₁

By invertendo, λ₂ / λ₁ = 1 / ( n₂ / n₁ )

λ₂ = λ₁ / ₁n₂

where ₁n₂ = refractive index of refractive mdeium with respect to incident medium. Let us assum that it is n.

λ₂ = λ₁ / n